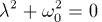
Die charakteristische Gleichung lautet:

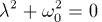
Die Lösungen sind:

Erklärung

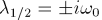
Die allgemeine Lösung der Differentialgleichung (ohne Anfangsbedingungen) lautet dann:

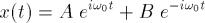
            wobei A  und B komplexe Werte annehmen können.

Erklärung

Die reelle Lösung des Anfangswertproblems lautet nun:

Erklärung

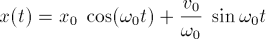
Haben Sie diese Aufgaben bewältigt, können Sie mit dem gedämpften harmonischen Oszillator fortfahren.