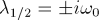
Man hat als Lösung der charakteristischen Gleichung:

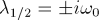
Das bedeutet, dass x(t) = exp (l t) für l = ± iw die Differentialgleichung löst.

man erhält also die beiden Lösungen

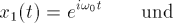
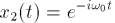
Man muss noch überprüfen, ob die beiden Funktionen linear unabhängig sind.

Es gelte also für alle t

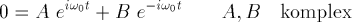
Zu zeigen: A=B=0

Für t = 0 gilt:

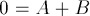
Für t = p/(2w) gilt:

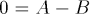
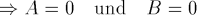
Aufgrund der Vektorraumeigenschaft der Lösungsmenge der Differentialgleichung gilt für jede Lösung der Differentialgleichung des harmonischen Oszillators:

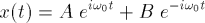
zurück zur Frage